Thuật toán về duyệt các thành phần liên thông của đồ thị bằng C/C++

Một đồ thị có thể liên thông hoặc không liên thông. Nếu đồ thị liên thông thì số thành phần liên thông của nó là 1. Điều này tương đương với phép duyệt theo thủ tục DFS() hoặc BFS() được gọi đến đúng một lần. Nếu đồ thị không liên thông (số thành phần liên thông lớn hơn 1) chúng ta có thể tách chúng thành những đồ thị con liên thông. Điều này cũng có nghĩa là trong phép duyệt đồ thị, số thành phần liên thông của nó bằng số lần gọi tới thủ tục DFS() hoặc BFS().

Để xác định số các thành phần liên thông của đồ thị, chúng ta sử dụng biến mới solt để nghi nhận các đỉnh cùng một thành phần liên thông trong mảng chuaxet[] như sau:

- Nếu đỉnh i chưa được duyệt, chuaxet[i]có giá trị 0;

- Nếu đỉnh i được duyệt thuộc thành phần liên thông thứ j=solt, ta ghi nhận chuaxet[i]=solt;

- Các đỉnh cùng thành phần liên thông nếu chúng có cùng giá trị trong mảng chuaxet[].

Với cách làm như trên, thủ tục BFS() có thể được sửa lại như sau:

void BFS(int u){

 queue = φ;

 u <= queue; /*nạp u vào hàng đợi*/

 solt = solt+1; chuaxet[u] = solt; /*solt là biến toàn cục thiết lập giá trị0*/

 while (queue ≠ φ) {

  queue<=p; /* lấy p ra từstack*/

  for v ∈ke(p) {

   if (chuaxet[v] ) {

    v<= queue; /*nạp v vào hàng đợi*/

    chuaxet[v] = solt; /* v có cùng thành phần liên thông với p*/

   }

  }

 }

}

Để duyệt hết tất cả các thành phần liên thông của đồ thị, ta chỉ cần gọi tới thủ tục liên thông như dưới đây:

void Lien_Thong(void){

 for (i=1; i≤n; i++)

  chuaxet[i] =0;

 for(i=1; i<=n; i++)

  if(chuaxet[i]==0){

   solt=solt+1;

   BFS(i);

  }

}

Để ghi nhận từng đỉnh của đồ thị thuộc thành phần liên thông nào, ta chỉ cần duyệt các đỉnh có cùng chung giá trị trong mảng chuaxet[] như dưới đây:

void Result( int solt){

 if (solt==1){

  < Do thi la lien thong>;

 }

 for( i=1; i<=solt;i++){

  /* Đưa ra thành phần liên thông thứi*/

  for( j=1; j<=n;j++){

   if( chuaxet[j]==i)

    <đưa ra đỉnh j>;

  }

 }

}

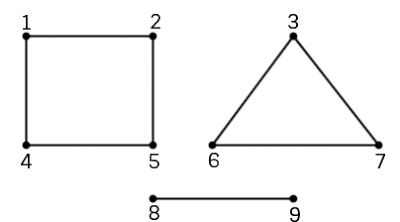
*Đỉnh 1,2,4,5 có giá trị 1trong mảng chuaxet[] thuộc thành phần liên thông thứ 1;

*Đỉnh 3, 6,7 cùng có giá trị 2 trong mảng chuaxet[] thuộc thành phần liên thông thứ 2;

*Đỉnh 8, 9 cùng có giá trị 3 trong mảng chuaxet[] thuộc thành phần liên thông thứ 3.

Chương trình cài đặt như sau:

#include<iostream>

#include <conio.h>

#define MAX  100

#define TRUE 1

#define FALSE 0

using namespace std;

int G[MAX][MAX], n, chuaxet[MAX], QUEUE[MAX], solt,i;


void Init(){

 freopen("lienth.IN", "r", stdin);

 cin>>n;

 cout<<" so dinh cua do thi n = "<<n;

 //nhập ma trận kề của đồ thị.

 for(int i=1; i<=n;i++){

  for(int j=1; j<=n;j++){

   cin>>G[i][j];

  }

 }

 //Khởi tạo giá trị ban đầu cho mảng chuaxet.

 for(int i=1; i<=n;i++)

  chuaxet[i]=0;

 solt=0;

}

void Result(int *chuaxet, int n, int solt){

 if(solt==1){

  printf("\n Do thi la lien thong");

  getch(); return;

 }

 for(int i=1; i<=solt;i++){

  printf("\n Thanh phan lien thong thu %d:",i);

  for(int j=1; j<=n;j++){

   if( chuaxet[j]==i)

    printf("%3d", j);

  }

 }

}

/* Breadth First Search */

void BFS(int G[][MAX], int n, int i, int *solt, int chuaxet[], int QUEUE[MAX]){

 int u, dauQ, cuoiQ, j;

 dauQ=1; cuoiQ=1;

 QUEUE[cuoiQ]=i;chuaxet[i]=*solt;

 while(dauQ<=cuoiQ){

  u=QUEUE[dauQ];

  dauQ=dauQ+1;

  for(j=1; j<=n;j++){

   if(G[u][j]==1 && chuaxet[j]==0){

    cuoiQ=cuoiQ+1;

    QUEUE[cuoiQ]=j;

    chuaxet[j]=*solt;

   }

  }

 }

}

void Lien_Thong(void){

 Init();

 for(i=1; i<=n; i++)

  if(chuaxet[i]==0){

   solt=solt+1;

   BFS(G, n, i, &solt, chuaxet, QUEUE);

  }

  Result(chuaxet, n, solt);

  _getch();

}

int main(void){

 Lien_Thong();

 return 0;

}

Dữ liệu file input lienth.IN như sau:

9

0 1 0 1 0 0 0 0 0

1 0 0 0 1 0 0 0 0

0 0 0 0 0 1 1 0 0

1 0 0 0 1 0 0 0 0

0 1 0 1 0 0 0 0 0

0 0 1 0 0 0 1 0 0

0 0 1 0 0 1 0 0 0

0 0 0 0 0 0 0 0 1

0 0 0 0 0 0 0 1 0

Trong đó: n = 9 là số đỉnh của đồ thị, tiếp theo đó là ma trận kề của đồ thị

Két quả khi chạy trương trình.

So dinh của do thi n = 9

Thanh phan lien thong thu 1: 1 2 4 5

Thanh phan lien thong thu 2: 3 6 7

Thanh phan lien thong thu 3: 8 9