Thuật toán về tìm kiếm theo chiều sâu DFS bằng ngôn ngữ C/C++

Để xem lý thuyết đồ thị với các định nghĩa về đường đi, chu trình, đồ thị liên thông bạn có thể xem ở đây.

>> Lý thuyết đồ thị - Đường đi - Chu trình - Đồ thị liên thông

Lý thuyết thuật toán tìm kiếm theo chiều rộng bạn có thể xem ở đây.

>> Lý thuyết thuật toán tìm kiếm theo chiều rộng BFS bằng C/C++ và Java

Tư tưởng cơ bản của thuật toán tìm kiếm theo chiều sâu là bắt đầu tại một đỉnh v0 nào đó, chọn một đỉnh u bất kỳ kề với v0 và lấy nó làm đỉnh duyệt tiếp theo. Cách duyệt tiếp theo được thực hiện tương tự như đối với đỉnh v0 với đỉnh bắt đầu là u.

Để kiểm tra việc duyệt mỗi đỉnh đúng một lần, chúng ta sử dụng một mảng chuaxet[] gồm n phần tử (tương ứng với n đỉnh), nếu đỉnh thứ i đã được duyệt, phần tử tương ứng trong mảng chuaxet[] có giá trị FALSE. Ngược lại, nếu đỉnh chưa được duyệt, phần tử tương ứng trong mảng có giá trị TRUE. Thuật toán có thể được mô tả bằng thủ tục đệ qui DFS () trong đó: chuaxet - là mảng các giá trị logic được thiết lập giá trị TRUE.

void DFS( int v){ 

 Thăm_Đỉnh(v);

 chuaxet[v]:= FALSE; 

 for ( u ∈ke(v) ) { 

  if (chuaxet[u] ) DFS(u); 

 } 

}

Thủ tục DFS() sẽ thăm tất cả các đỉnh cùng thành phần liên thông với mỗi đỉnh đúng một lần. Để đảm bảo duyệt tất cả các đỉnh của đồ thị (có thể có nhiều thành phần liên thông), chúng ta chỉ cần thực hiện duyệt như sau:

for (i=1; i≤n ; i++)

 chuaxet[i]:= TRUE; /* thiết lập giá trị ban đầu cho mảng chuaxet[]*/

for (i=1; i≤n ; i++)

 if (chuaxet[i] )

  DFS( i);

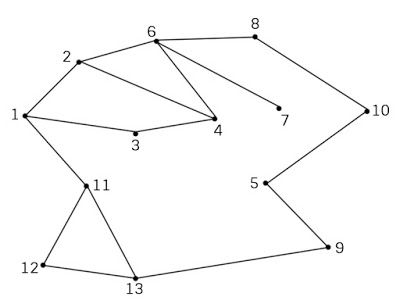
Đồ thị - Tìm kiếm theo chiều sâu DFS

Kết quả duyệt: 1, 2, 4, 3, 6, 7, 8, 10, 5, 9, 13, 11, 12

DFS.IN

13
0    1    1    0    0    0    0    0    0    0    1    0    0
1    0    0    1    0    1    0    0    0    0    0    0    0
1    0    0    1    0    0    0    0    0    0    0    0    0
0    1    1    0    0    1    0    0    0    0    0    0    0
0    0    0    0    0    0    0    0    1    1    0    0    0
0    1    0    1    0    0    1    1    0    0    0    0    0
0    0    0    0    0    1    0    0    0    0    0    0    0
0    0    0    0    0    1    0    0    0    1    0    0    0
0    0    0    0    1    0    0    0    0    0    0    0    1
0    0    0    0    1    0    0    1    0    0    0    0    0
1    0    0    0    0    0    0    0    0    0    0    1    1
0    0    0    0    0    0    0    0    0    0    1    0    1
0    0    0    0    0    0    0    0    1    0    1    1    0

Chương trình cài đặt bằng C/C++

#include<iostream>

#include<conio.h>

using namespace std;

#define MAX  100 

#define TRUE 1 

#define FALSE 0 

int G[MAX][MAX], n, chuaxet[MAX]; 

void Init(){ 

 freopen("DFS.IN", "r", stdin); 

 cin>>n; 

 cout<<"So dinh cua ma tran n = "<<n<<endl;

 //nhap ma tran lien ke.

 for(int i=1; i<=n;i++){ 

  for(int j=1; j<=n;j++){ 

   cin>>G[i][j]; 

  } 

 } 

} 

/* Depth First Search */

void DFS(int G[][MAX], int n, int v, int chuaxet[]){ 

 cout<<"Duyet dinh : "<<v<<endl;

 int u; 

 chuaxet[v]=FALSE; 

 for(u=1; u<=n; u++){ 

  if(G[v][u]==1 && chuaxet[u]) 

   DFS(G,n, u, chuaxet); 

 } 

} 

void main(void){ 

 Init(); 

 for(int i=1; i<=n; i++) 

  chuaxet[i]=TRUE; 

 for(int i=1; i<=n;i++) 

  if(chuaxet[i]) 

   DFS( G,n, i, chuaxet); 

 _getch(); 

}

Chương trình cài đặt bằng Java.

package simplecodecjava.blogspot.com;

import java.io.BufferedReader;

import java.io.File;

import java.io.FileNotFoundException;

import java.io.FileReader;

import java.io.IOException;


public class DFSAlgorithm {

 static final int MAX = 100;

 int G[][] = new int[MAX][MAX];// matran kề.

 int n = 0; // số dỉnh của đồ thị

 boolean chuaxet[] = new boolean[MAX];// mảng đánh dấu đỉnh đã được thăm.

 void Init() {

  File file = new File(getClass().getResource("DFS.IN").getPath());

  BufferedReader reader = null;

  try {

   reader = new BufferedReader(new FileReader(file));

   n = Integer.parseInt(reader.readLine());

   for (int i = 1; i <= n; i++) {

    String[] aLineOfMatrix = reader.readLine().split("\\s+");

    for (int j = 1; j <= n; j++) {

     G[i][j] = Integer.parseInt(aLineOfMatrix[j -1]);// index của J bắt đầu từ 0.

    }

   }

  }catch(FileNotFoundException e){

   e.printStackTrace();

  } catch (IOException e) {

   e.printStackTrace();

  }

  finally {

   if (reader != null)

    try {

     reader.close();

    } catch (IOException e) {

     e.printStackTrace();

    }

  }

 }


 void DFS(int v) {

  int u;

  System.out.print(v + " ");

  chuaxet[v] = false;

  for (u = 1; u <= n; u++) {

   if (G[v][u] == 1 && chuaxet[u])

    DFS(u);

  }

 }


 public DFSAlgorithm() {

  Init();

  for (int i = 1; i <= n; i++){

   chuaxet[i] = true;

  }

  System.out.print("\n");

  for (int i = 1; i <= n; i++)

   if (chuaxet[i]){

    DFS(i);

   }

 }


 public static void main(String[] args) {

  System.out.println("DFS");

  new DFSAlgorithm();

 }

}