Thuật toán về tìm đường đi và chu trình Hamilton cài đặt bằng C/C++

Để xem lý thuyết đồ thị với các định nghĩa về đường đi, chu trình, đồ thị liên thông bạn có thể xem ở đây.

>>> Lý thuyết đồ thị - Đường đi - Chu trình - Đồ thị liên thông

Với đồ thị Euler, chúng ta quan tâm tới việc duyệt các cạnh của đồ thị mỗi cạnh đúng một lần, thì trong mục này, chúng ta xét đến một bài toán tương tự nhưng chỉ khác nhau là ta chỉ quan tâm tới các đỉnh của đồ thị, mỗi đỉnh đúng một lần. Sự thay đổi này tưởng như không đáng kể, nhưng thực tếcó nhiều sự khác biệt trong khi giải quyết bài toán.

Định nghĩa. Đường đi qua tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần được gọi là đường đi Hamilton. Chu trình bắt đầu tại một đỉnh v nào đó qua tất cả các đỉnh còn lại mỗi đỉnh đúng một lần sau đó quay trở lại v được gọi là chu trình Hamilton. Đồ thị được gọi là đồ thị Hamilton nếu nó chứa chu trình Hamilton. Đồ thị chứa đường đi Hamilton được gọi là đồ thị nửa Hamilton.

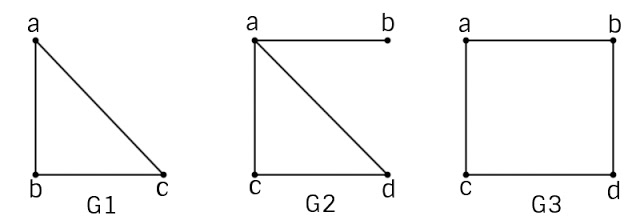
Như vậy, một đồ thị Hamilton bao giờ cũng là đồ thị nửa Hamilton nhưng điều ngược lại không luôn luôn đúng. Ví dụ sau sẽ minh họa cho nhận xét này.

Ví dụ. Đồ thị hamilton G1, G3, nửa Hamilton G2.

Cho đến nay, việc tìm ra một tiêu chuẩn để nhận biết đồ thị Hamilton vẫn còn mở, mặc dù đây là vấn đề trung tâm của lý thuyết đồ thị. Hơn thế nữa, cho đến nay cũng vẫn chưa có thuật toán hiệu quả để kiểm tra một đồ thị có phải là đồ thị Hamilton hay không.

Để liệt kê tất cả các chu trình Hamilton của đồ thị, chúng ta có thể sử dụng thuật toán sau:

void Hamilton( int k) { 

 /* Liệt kê các chu trình Hamilton của đồ thị bằng cách phát triển dãy đỉnh 

 (X[1], X[2],..., X[k-1] ) của đồ thị G = (V, E) */

 for y∈Ke(X[k-1]) { 

  if (k==n+1) and (y == v0) then 

   Ghinhan(X[1], X[2],..., X[n], v0); 

  else { 

   X[k]=y; chuaxet[y] = false; 

   Hamilton(k+1); 

   chuaxet[y] = true; 

  } 

 } 

}

Chương trình chính được thể hiện như sau:

for (v∈V ) chuaxet[v] = true; /*thiết lập trạng thái các đỉnh*/

 X[1] = v0; (*v0 là một đỉnh nào đó của đồ thị*) 

 chuaxet[v0] = false; 

 Hamilton(2);

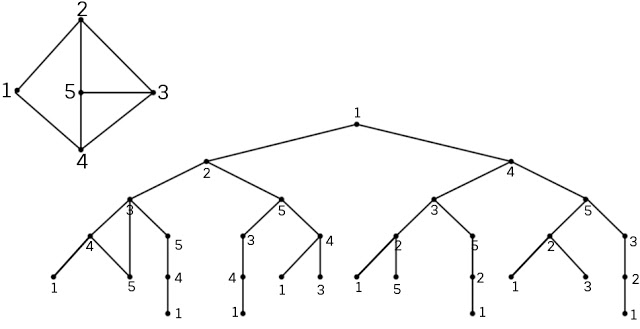
Cây tìm kiếm chu trình Hamilton thể hiện thuật toán trên được mô tả như sau:

Chương trình liệt kê các chu trình Hamilton được thể hiện như sau:

#include<iostream>

#include<conio.h>

using namespace std;

#define MAX 50 

#define TRUE 1 

#define FALSE  0 

int A[MAX][MAX];//ma trận liền kề.

int C[MAX], B[MAX]; 

int n;//số đỉnh của đồ thị.

int d;//đếm số lượng chu trình hamilton.

void Init(void){ 

 freopen("CCHMTON.IN", "r",stdin); 

 cin>>n; 

 //nhập ma trận kề

 for(int i=1; i<=n; i++){ 

  for(int j=1; j<=n; j++){ 

   cin>>A[i][j]; 

  } 

 } 

 for (int i=1; i<=n;i++) 

  C[i]=0; 

} 

void Result(void){ 

 cout<<"Chu trinh Hamilton: ";

 for(int i=n; i>=0; i--) 

  cout<<B[i]<<" "; 

 d++; 

 cout<<endl;

} 

void Hamilton(int *B, int *C, int i){ 

 int j, k; 

 for(j=1; j<=n; j++){ 

  if(A[B[i-1]][j]==1 && C[j]==0){ 

   B[i]=j; C[j]=1; 

   if(i<n) Hamilton(B, C, i+1); 

   else

    if(B[i]==B[0]) Result(); 

   C[j]=0; 

  } 

 } 

} 

void main(void){ 

 B[0]=1; 

 int i=1;

 d=0;

 Init(); 

 Hamilton(B,C,i); 

 if(d==0) 

  cout<<"Khong co chu trinh Hamilton"; 

 getch(); 

} 

Ma trận liền kề của đồ thị:

5

0 1 0 1 0

1 0 1 0 1

0 1 0 1 1

1 0 1 0 1

0 1 1 1 0

Output của chương trình:

Chu trinh Hamilton: 1 4 5 3 2 1

Chu trinh Hamilton: 1 4 3 5 2 1

Chu trinh Hamilton: 1 2 5 3 4 1

Chu trinh Hamilton: 1 2 3 5 4 1

Chương trình duyệt tất cả đường đi Hamilton như sau:

#include<iostream>

#include<conio.h>

using namespace std;

#define MAX 50 

#define TRUE 1 

#define FALSE  0 

int A[MAX][MAX];//ma trận kề của đồ thị.

int C[MAX], B[MAX];//mảng đánh dấu.

int n;//số đỉnh của đồ thị.

int d;//đếm số đường đi Hamilton.

void Init(void){ 

 freopen("DDHMTON.IN", "r",stdin); 

 cin>>n; 

 //nhập ma trận liền kề.

 for(int i=1; i<=n; i++){ 

  for(int j=1; j<=n; j++){ 

   cin>>A[i][j]; 

  } 

 } 

 for (int i=1; i<=n;i++) 

  C[i]=0; 

} 

void Result(void){ 

 cout<<"Duong di Hamilton: ";

 for(int i=n; i>0; i--) 

  cout<<B[i]<<" "; 

 d++; 

 cout<<endl;

} 

void Hamilton(int *B, int *C, int i){ 

 int j, k; 

 for(j=1; j<=n; j++){ 

  if(A[B[i-1]][j]==1 && C[j]==0){ 

   B[i]=j; C[j]=1; 

   if(i<n) Hamilton(B, C, i+1); 

   else Result(); 

   C[j]=0; 

  } 

 } 

} 

void main(void){ 

 B[0]=1; 

 int i=1;

 d = 0;

 Init(); 

 Hamilton(B,C,i); 

 if(d==0) 

  cout<<"Khong co duong di Hamilton"; 

 getch(); 

}

}