Tập tành tìm hiểu Thuật toán Support Vector Machine – SVM

SVM là gì?

SVM (Support Vector Machine) là một thuật toán học máy có giám sát được sử dụng rất phổ biến ngày nay trong các bài toán phân lớp (classification) hay hồi qui (Regression).

SVM được đề xuất bởi Vladimir N. Vapnik và các đồng nhiệp của ông vào năm 1963 tại Nga và sau đó trở nên phổ biến trong những năm 90 nhờ ứng dụng giải quyết các bài toán phi tuyến tính (nonlinear) bằng phương pháp Kernel Trick.

SVM hay SVMs?

Khi đọc các tài liệu về SVM các bạn thường thấy SVM và SVMs đều được nhắc đến vậy chúng khác nhau thế nào. Thực chất SVM và SVMs là một. Người ta dùng SVMs là vì muốn nói đến hai loại của thuật toán của SVM:

• SVM: dùng cho các bài toán phân lớp
• SVR (Support Vector Regression): dùng cho các bài toán hồi quy

Theo kinh nghiệm của mình thấy thì việc ứng dụng SVM để giải quyết các bài toán thực tế thường cho kết quả cao so với các thuật toán ML khác đặc biệt là các bài toán phân loại liên quan đến xử lý văn bản. Có lẽ chính vì vậy mà SVM có một nền tảng toán học và lý thuyết khá phức tạp. Trong bài này mình chỉ giới thiệu một cách tổng quan về cách thức hoạt động của SVM còn về các khía cạch toán học khác mình sẽ giải thích kỹ hơn ở một bài khác.

Để hiểu được một cách đầy đủ về SVM trong các bài toán thực tế chúng ta cần nắm được các bài toán con của SVM: linear, hard-margin, soft-margin, non-linear, binary-class và multi-class. Mình sẽ giải thích rõ từng vấn đề này.

SVM làm việc như thế nào?

Ý tưởng của SVM là tìm một siêu phẳng (hyper lane) để phân tách các điểm dữ liệu. Siêu phẳng này sẽ chia không gian thành các miền khác nhau và mỗi miền sẽ chứa một loại giữ liệu.

Siêu phẳng được biểu diễn bằng hàm số  ( W và X là các vector <W.X> là tích vô  ) Hay  (  là ma trận chuyễn vị)

Vấn đề là có rất nhiều siêu phẳng, chúng ta phải chon cái nào để tối ưu nhất ?

Cách chọn siêu phẳng tối ưu:

Giả sử chúng ta phải phân loại tập dữ liệu các lớp dương  (màu xanh) nhãn là 1 và các dữ liệu lớp âm (màu đỏ) nhãn là -1 (tập dữ liệu có thể phân tách tuyến tính).

Siêu phẳng phân tách hai lớp giữ liệu $H_0$ thỏa mã <W.X> + b =0. Siêu phẳng này tạo ra hai nữa không gian (half space) dữ liệu:
Không gian các dữ liệu lớp âm $X_i$ thỏa mãn   và không gian dữ liệu lớp dương $X_j$ thỏa mãn  

Tiếp theo ta chọn hai siêu phẳng lề $H_1$ đi qua điểm thuộc lớp âm và $H_2$ đi qua điểm thuộc lớp dương đều song song với $H_0$

• $H_1$:  <W.X> + b =-1
• $H_2$:  <W.X> + b =1

Khoảng cách từ $H_1$ đến $H_0$ là $d_{-}$

Khoảng cách từ $H_2$ đến $H_0$ là $d_{+}$

m = $d_{-} + d_{+}$ được gọi là mức lề

Siêu phẳng tối ưu mà chúng ta cần chọn là siêu phẳng phân tách có lề lớn nhất. Lý thuyết học máy đã chỉ ra rằng một siêu phẳng như vậy sẽ cực tiểu hóa giới hạn lỗi mắc phải.

Tính m (margin) như thế nào ?

Khoảng cách từ một điểm $X_k$ đến siêu phẳng $H_0$ là: $\frac{|<W.X_k>+ b|}{\left|\right|W\left|\right|}$  Trong đó ||W|| là độ dài của vector W: $\left|\right|W\left|\right| = <W.W> = \sqrt{{w_1}^2 +{w_2}^2 + ...{w_n}^2}$  

Khoảng cách từ một điểm $X_i$ nằm trên $H_1$ đến $H_0$    $d_{-} = \frac{|<W.X_i>+ b|}{\left|\right|W\left|\right|} = \frac{1}{\left|\right|W\left|\right|}$ 
Khoảng cách từ một điểm $X_j$ nằm trên $H_2$ đến $H_0$    $d_{+} = \frac{|<W.X_j>+ b|}{\left|\right|W\left|\right|} = \frac{1}{\left|\right|W\left|\right|}$ 
Từ đó ta có thể tính được mức lề   $m = d_{-} + d_{+} = \frac{2}{\left|\right|W\left|\right|}$ 

Giờ thì bạn đã hiểu vì sao các điểm nằm trên hai siêu phẳng $H_1$ và $H_2$ được gọi là các Support Vector.

Vậy việc training trong giải thuật SVM tương được với bài toán cực tiểu hóa có ràng buộc sau đây :

Cực tiểu hóa :  $\frac{<W.W>}{2}$ 

Với điều kiện: $\left\{\begin{array}{ll}<W.X_i> + b \le -1& if y_i = -1 \left(1\right)\\ <W.X_i> + b \ge 1 & if y_i = 1 \left(2\right)\end{array}\right.$
Nhân hai vế bất đẳng thức của (1) và (2) với $y_i$ ta được điều kiện thu gọn $y_i.(<W.X_i>) \ge 1 \forall i = 1..n$

Bài toán tương đương với

Minimize: ||W||

Subject to : $y_i.(<W.X_i>) \ge 1 \forall i = 1..n$ (3)

Với điều kiện này, đây chính là bài toán hard-margin của SVM

Việc giải bài toán trên liên quan đến một số lý thuyết toán học tương đối phức tạp như điều kiện Karush-Kuhn-Tucker, hàm đối ngẫu Lagrange, Convex optimization … Mình sẽ không nói ở bài này.

Việc xác định siêu phẳng $H_0$ được giả sử trong điều kiện lý tưởng tập dữ liệu có thể phân tách tuyến tính, tìm được hai siêu phẳng lề $H_1$ và $H_2$ mà không có điểm dữ liệu nào nằm giữa chúng. Vậy trong trường hợp tập dữ liệu có nhiều điểm gây nhiễu, các điểm này không thỏa mãn điều kiện (3), bài toán không tìm được lời giải.

Đối với các trường hợp này chúng ta cần nới lỏng các điều kiện lề bằng việc sử dụng các biến slack ${\epsilon }_i \ge 0$

$<W.X_i> + b \le -1 + {\epsilon }_i if y_i = -1$

$<W.X_i> + b \ge 1 - {\epsilon }_i if y_i = -1$

Bài toán trong trường hợp này trở thành:

Minimize: $\left|\right|W\left|\right| + C\sum _{i = 1}^n{\epsilon }_i$
Subject to: $\left\{\begin{array}{l}{y}_i .(<W.X_i>) \ge 1 - {\epsilon }_i, \forall i = 1..n\\ {\epsilon }_i \ge 0, \forall i = 1..n\end{array}\right.$ 

Trong đó C là tham số xác định mức độ phạt của (penalty degree) đối với các lỗi (đây là mà một tham số khá quan trọng mà các bạn cần phải tối ưu trong quá trình huấn luyện SVM)
Đây chính là bài toán Soft-margin của SVM.

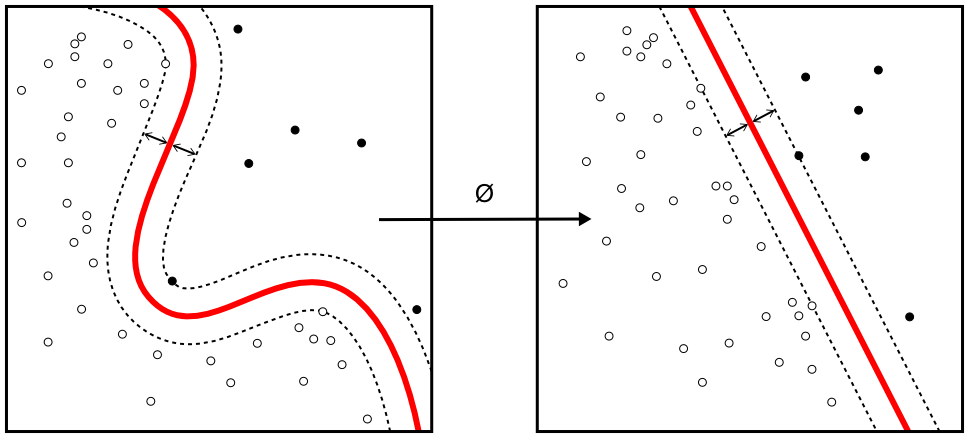
Một vấn đề cuối cùng mà mình muốn nhắc đến trong bài này là đối với các bài toán có không gian dữ liệu là phi tuyến tính (non-linear) chúng ta không thể tìm được một siêu phẳng  thỏa mãn bài toán.

Để giải quyết bài toán trong trường hợp này chúng ra cần biểu diễn (ánh xạ ) dữ liệu từ không gian ban đầu X sang không gian F bằng một hàm ánh xạ phi tuyến:

$$\begin{gathered} \varphi : X \to F \\ x \to \varphi \left(x\right) \end{gathered}$$

Trong không gian F tập dữ liệu có thể phân tách tuyến tính. Nhưng nãy sinh một vẫn đề lớn đó là trong không gian mới này số chiều của giữ liệu tăng lên rất nhiều so với không gian ban đầu làm cho chi phí tính toán vô cùng tốn kém.  Rất may trong bài toán SVM người ta đã tìm ra một cách không cần phải tính $\varphi \left(x\right), \varphi \left(z\right)$ và hàm ánh xạ $\varphi$ mà vẫn tính được $<\varphi \left(x\right).\varphi \left(z\right)>$.  Phương pháp này gọi là Kernel Trick

$K(x,z) = <\varphi \left(x\right).\varphi \left(z\right)>$ K(x,z) là một hàm nhân (Kernel functions)

Một số hàm nhân thường dùng:

• Polynomial: $K(x,z) = {(<x,z> + \varphi )}^d$
• Gaussian RBF: $K(x,z) = e^{\frac{\left|\right|x - z|{|}^2}{2\delta }}; \delta >0$
• Sigmoidal: $\tan (\beta <x, z >-\lambda ) = \frac{1}{1 + e^{-(\varphi <x,z> - \lambda )}}; \beta ,\lambda \in R$

Tóm lại: trong bài này mình trình bày các khái niệm, ý tưởng và cách hoạt động cơ bản của giải thuật SVM để các bạn có thể hiểu rõ hơn và là bước đệm (:D) để tìm hiểu sâu hơn về nền tảng toán học của nó . Một số địa chỉ để các bạn có thể tìm hiểu thêm về SVM:

• svm-tutorial.com
• machinelearningcoban.com