1. Cộng 2 số nhị phân
Xem trong bài Chuyển đổi số từ thập phân sang nhị phân
2. Trừ 2 số nhị phân
Để trừ 2 số nhị phân, ta cần nhớ các nguyên tắc sau:
-
0 − 0 = 0
-
0 − 1 = −1 (mượn)
-
1 − 0 = 1
-
1 − 1 = 0
-
-1-1 = -10
Ví dụ 1: ta thực hiện phép trừ sau 10 – 8 = 2
Ta có số 1010=10102, số 810=10002
|
Cột |
4 |
3 |
2 |
1 |
|
10= |
1 |
0 |
1 |
0 |
|
8= |
1 |
0 |
0 |
0 |
|
|
2= |
0 |
0 |
1 |
0 |
Ví dụ 2: Thực hiện phép trừ 51 – 28 = 23
Số 5110 = 1100112, số 2810 = 111002
|
Cột |
6 |
5 |
4 |
3 |
2 |
1 |
|
51 = |
1 |
1 |
0 |
0 |
1 |
1 |
|
28 = |
0 |
1 |
1 |
1 |
0 |
0 |
|
|
23 = |
0 |
1 |
0 |
1 |
1 |
1 |
Ta tiến hành trừ từ phải sang trái như sau (chú ý màu sắc các kí số 0 và 1 để dễ hiểu hơn):
|
Bước |
Tại cột |
Thực hiện phép tính |
|
1 |
1 |
1 – 0 = 1 |
|
2 |
2 |
1 – 0 = 1 |
|
3 |
3 |
0 – 1 = -1 , viết 1 và nhớ -1 |
|
4 |
4 |
0 – 1 = -1, cộng với -1 ở bước 3 là -10, viết 0 và nhớ -1 |
|
5 |
5 |
1 – 1 = 0, cộng với -1 ở bước 4 là -1, viết 1 và nhớ -1 |
|
6 |
6 |
1 cộng với -1 ở bước 5 là 0 |
Vậy 110011 – 11100 = 010111 (tương ứng với 51 – 28 = 23)
Số bù 1:
Khi ta đảo tất cả các bit có trong số nhị phân (đổi 1 thành 0 và ngược lại), ta có số bù 1 của số nhị phân đó. Số bù 1 thường được dùng để biểu diễn số âm trong máy tính. Khi đó, bit cực trái (bit đầu tiên ở bên trái) là bit đánh dấu với qui ước: nếu bit dấu là 0 thì số là số dương, nếu bit dấu là 1 thì là số âm.
Ví dụ: số 28 trong hệ thập phân biểu diễn sang nhị phân (với mẫu 8 bit) là 0001 1100. Vậy số bù 1 sẽ là 1110 0011.
Để thực hiện phép trừ với số nhị phân, ta có thể thực hiện phép cộng với số bù 1 của số nhị phân đó.
Ví dụ: Thực hiện phép trừ 2 – 5 = -3
Ta có 210 = 0000 00102
510= 0000 01012. Số bù 1 của 5 là 1111 1010.
Vậy 2 – 5 = 0000 0010 + 1111 1010
|
Cột |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
2 = |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
-5 = |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Ta thực hiện phép cộng như sau:
|
Bước |
Tại cột |
Thực hiện phép tính |
|
1 |
1 |
0 + 0 = 0 |
|
2 |
2 |
1+ 1 = 10, viết 0 nhớ 1 |
|
3 |
3 |
0 + 0 = 0, cộng với 1 nhớ ở bước 2 là 1 |
|
4 |
4 |
0 + 1 = 1 |
|
5 |
5 |
0 + 1 = 1 |
|
6 |
6 |
0 + 1 = 1 |
|
7 |
7 |
0 + 1 = 1 |
|
8 |
8 |
0 + 1 = 1 |
Ta được kết quả 1111 1100.
Ví dụ: Thực hiện phép trừ 51 – 28 = 23
Số 5110= 0011 00112. Số 2810 = 0001 11002, số bù 1 là 1110 0011.
51 – 28 = 51 + (-28) = 0011 0011 + 1110 0011
|
Cột |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
51 = |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
-28 = |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
|
0 (nhớ 1) |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Ta thực hiện phép cộng như sau:
|
Bước |
Tại cột |
Thực hiện phép tính |
|
1 |
1 |
1 + 1 = 10, viết 0, nhớ 1 |
|
2 |
2 |
1 + 1 = 10, cộng thêm 1 (nhớ ở bước 2) là 11, viết 1 nhớ 1 |
|
3 |
3 |
0 + 0 = 0, cộng 1 (nhớ ở bước 2) là 1 |
|
4 |
4 |
0 + 0 = 0 |
|
5 |
5 |
1 + 0 = 1 |
|
6 |
6 |
1 + 1 = 10, viết 0 nhớ 1 |
|
7 |
7 |
0 + 1 = 1, cộng thêm 1 (nhớ ở bước 6) là 10, viết 0 nhớ 1 |
|
8 |
8 |
0 + 1 = 1, cộng thêm 1 (nhớ ở bước 7) là 10, viết 0 và nhớ 1. |
Ta được kết quả 0001 0110, và ta thấy ở bước 8 vẫn còn nhớ 1, ta cộng số 1 này vào bit cực phải của kết quả 0001 0110, nghĩa là 0001 0110 +1 và được 0001 0111.
Số bù 2:
Số bù 2 có được là do đảo tất cả các bit có trong số nhị phân (đổi 1 thành 0 và đổi 0 thành 1) rồi cộng thêm 1 vào kết quả. Hay nói cách khác, số bù 2 là số bù 1 cộng thêm 1. Số bù 2 cũng được dùng để biểu diễn số âm. Khi đó, bit cực trái (bit đầu tiên ở bên trái) là bit đánh dấu với qui ước: nếu bit dấu là 0 thì số là số dương, nếu bit dấu là 1 thì là số âm.
Ví dụ: Thực hiện phép trừ 2 – 5 =-3
Ta có 210 = 0000 00102
510= 0000 01012. Số bù 1 của 5 là 1111 1010, số bù 2 của 5 là 1111 1011
Vậy 2 – 5 = 0000 0010 + 1111 1011
|
Cột |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
2= |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
-5 = |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
Ta thực hiện phép cộng như sau:
|
Bước |
Tại cột |
Thực hiện phép tính |
|
1 |
1 |
0 + 1 =1 |
|
2 |
2 |
1 + 1 = 10, viết 0 nhớ 1 |
|
3 |
3 |
0 + 0 = 0, cộng 1 nhớ ở bước 2 là 1 |
|
4 |
4 |
0+ 1 = 1 |
|
5 |
5 |
0 + 1 = 1 |
|
6 |
6 |
0 + 1 = 1 |
|
7 |
7 |
0 + 1 = 1 |
|
8 |
8 |
0 + 1 = 1 |
Ta được kết quả 1111 1101, là số bù 2 của -3
3. Nhân hai số nhị phân
Phép tính nhân trong hệ nhị phân cũng tương tự như phương pháp làm trong hệ thập phân. Hai số A và B được nhân với nhau bởi những tích số của các kí số 0 và 1 của A và B: với mỗi con số ở B, tích của nó với số một con số trong A được tính và viết xuống một hàng mới, mỗi hàng mới phải chuyển dịch vị trí sang bên trái 1 bit. Tổng của các tích cục bộ này cho ta kết quả tích số cuối cùng.
Ví dụ: 9 x 6 = 54 (1001 x 110 = 110110)
Để dễ hiểu, bạn xem 2 hình dười đây, hình thứ nhất biểu diễn cách nhân 2 số thập phân và hình thứ 2 là cách nhân 2 số nhị phân.

Nhân 2 số thập phân

Nhân 2 số nhị phân
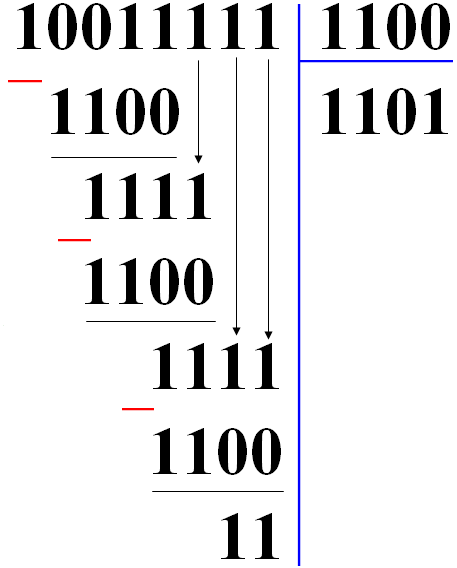
4. Chia 2 số nhị phân
Phép chia số nhị phân tương đối phức tạp hơn phép cộng, trừ và nhân. Cách chia số nhị phân cũng giống như chia 2 số thập phân, do đó các bạn cần nắm vững cách chia trên số thập phân, đồng thời cần nắm vững cách trừ 2 số nhị phân. Đầu tiên hãy xem hình 1 để nhớ lại cách chia 2 số thập phân, sau đó xem hình 2 các bạn sẽ hiểu cách chia số nhị phân.

Chia 2 số thập phân

Chia 2 số nhị phân































![Viết chương trình in ra các số bậc thang trong đoạn [n1, n2] với n1, n2 được nhập từ bàn phím. Viết chương trình in ra các số bậc thang trong đoạn [n1, n2] với n1, n2 được nhập từ bàn phím.](https://expressmagazine.net/sites/default/files/styles/thumbnail/public/imageDevelopment/viet-chuong-trinh-in-ra-cac-so-bac-thang-trong-doan.jpg?itok=mimCbEcT)
